Diferentes métodos para calcular decimales de π automatizados con python.

Introducción

Todos los lectores ya conocerán el número π, definido por el perímetro de cualquier círculo entre su diámetro. Lo cierto es que este es conocido desde la antigüedad y ya entonces antiguos matemáticos trataban de conseguir una aproximación, pero estos usaban métodos de medición para conseguirla, es decir mediante mediciones, lo que unicamente les permitió avanzar de manera muy limitada, por la precisión tanto de la medida como del trazo del círculo.

• Mesopotámicos π≈3.1428
• Egipcios π≈3.16049

Este caso es un claro ejemplo de un problema que parece sencillo al inicio, pero que en realidad necesita de muchas matemáticas para ser resuelto. Hoy veremos 3 diferentes soluciones a este problema.

Método de Arquímedes

Como podemos ver en la siguiente animación, cuantos más lados tiene un polígono regular más se asemeja a una circunferencia.

La diferencia es clara, para calcular el perímetro polígono no nos es necesario π, por tanto una vez calculado dividiremos entre el doble del radio de este y obtendremos una aproximación de π.

#El código usa polígonos de ángulos iguales para simplificar el programa 

import math
import sys

radio = 1
ladoinicial = 1
nlados = 12
sys.setrecursionlimit(100)

iteraciones=int(input("Iteraciones> " ))
def SiguienteLado(lado):
    global nlados
    global iteraciones
    
    if iteraciones != 0:
        global radio
        apotema=math.sqrt(1-(lado/2)**2)
        cateto1=radio-apotema
        cateto2=lado/2
        ladonuevo=math.sqrt((cateto1)**2+(cateto2)**2)
        print("Numero de lados "+str(nlados)+">   "+str((nlados*ladonuevo)/2*radio))
        nlados=nlados*2
        iteraciones-=1
        SiguienteLado(ladonuevo)

SiguienteLado(ladoinicial)

Método de Montecarlo

Este método es genial para estimar el área de figuras complejas de evaluar con exactitud, se usa por ejemplo como método de integración, funciona mediante números aleatorios, o en este caso pseudoaleatorios. Supongamos una circunferencia de radio r inscrita en un cuadrado, el cociente entre sus áreas será:

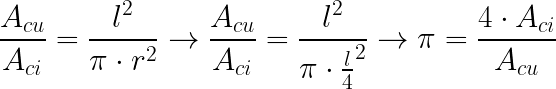
de donde se despeja que π es igual al cociente entre cuatro veces el área del circulo entre el área del cuadrado.

Como vemos en la animación el método consiste en elegir puntos aleatórios dentro de este cuadrado, todos entrarán en el cuadrado pero no todos en el círculo.

La idea tras esto es que depués de marcar una gran cantidad de puntos aleaorios por pura estadística el cociente entre los puntos del cuadrado y del círculo equivale al cociente entre sus áreas.

En Python con GUI

import tkinter as tk
import random
import sys


dentro=[]
fuera=[]
sys.setrecursionlimit(10000000)
numerodepuntos=int(input("Cantidad de puntos> "))

def randompoint(numbers):

    if numbers==0:

        print(((len(dentro)/(len(dentro)+len(fuera))*4)))
        print(len(fuera), len(dentro))
    else:
        a=random.randint(1,500)
        b=random.randint(1,500)

        canvas.create_oval(a, b, a+10, b+10, width=5, fill="blue")
        if ((250-a)**2+(250-b)**2)**0.5 <= 250:
            dentro.append("1")
        else:
            fuera.append("1")
        canvas.after(1, randompoint, numbers-1)

window=tk.Tk()
canvas=tk.Canvas(window, width=500, height=500, background="black")
canvas.grid(column=0, row=0)
canvas.create_oval(0, 0, 500, 500, width=5, fill="red")

canvas.after(10, randompoint, numerodepuntos)

window.mainloop()

En C

#include <stdio.h>
#include <math.h>

int main()
{
    long int puntos;
    long int Pcirculos=0;
    printf("Numero de puntos> ");
    scanf("%ld", &puntos);
    srand(time_t(NULL));
    int i=0;
    for (i; i<puntos; i++){

        int a = rand() % 500;
        int b = rand() % 500;

        int c=sqrt(pow((a-250), 2)+pow((b-250), 2));

        if (c<=250){
            Pcirculos+=1;
        }
    }
    float res1 = 4*((float)Pcirculos/(float)puntos);
    printf("%d\n", puntos);
    printf("-----------------\n");
    printf("%d\n", Pcirculos);
    printf("Aprox> %f", res1);
    return 0;
}

Series

Por último las series, sin duda el método más eficiente para calcular pi, existen una gran cantidad de estas algunas mejores que otras hoy vamos a aplicar la serie de Ramanujan-Sato. Simplemente calculamos mediante infinitas iteraciones de la siguiente suma infinita:

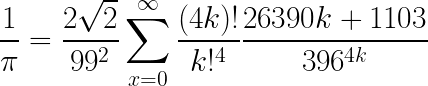
from decimal import *
import math

precision=int(input("Máximo de dígitos> "))
iteraciones=int(input("Numero de iteraciones> "))
getcontext().prec = precision

a=(Decimal(2)*(Decimal(2)**Decimal(0.5)))/Decimal(9801)
b=0

for k in range(0,iteraciones):
    
    numerador=math.factorial(4*k) * (1103 + 26390*k)

    denominador=(math.factorial(k)**4) * 396**(4*k)
    b+=Decimal(a)*Decimal(numerador)/Decimal(denominador)
    
print(1/Decimal(b))

Notas finales

En este post, hemos explorado tres métodos diferentes para calcular el valor de π de manera automatizada utilizando Python y C. Cada uno de estos métodos tiene sus propias ventajas y aplicaciones.

El Método de Arquímedes nos muestra cómo la geometría y la recursión pueden llevarnos a una aproximación de π al dividir el perímetro de polígonos regulares entre el doble del radio de una circunferencia inscrita.

El Método de Montecarlo, por otro lado, nos demuestra cómo los números aleatorios pueden ayudarnos a estimar π calculando el área de una circunferencia inscrita en un cuadrado. Esta técnica se usa ampliamente en computación científica.

Finalmente, las Series nos brindan un enfoque más sofisticado y preciso para calcular π. La serie de Ramanujan-Sato, en particular, nos permite obtener resultados altamente precisos a medida que aumentamos la cantidad de iteraciones.